在交易领域，组合数学与概率论为复杂交易系统的构建提供了坚实的数学基础。本文将结合MetaTrader5安卓版，从理论框架、数学建模到实际应用，系统阐述这一分析方法的核心逻辑与实践价值。

　　一、组合数学与概率论的基础作用

　　1. 组合数学在策略优化中的应用

　　组合数学通过量化资产相关性、计算概率分布，帮助交易者构建风险分散的投资组合。例如，通过计算不同资产间的协方差矩阵，可优化权重分配以降低整体波动性。在高频交易中，组合数学还可用于设计订单路由算法，提升系统吞吐量。

　　2. 概率论驱动的交易决策

　　概率论为交易者提供了评估不确定性的量化工具。例如，通过定义“市场清晰系数”（MCI）衡量交易者对市场状态的认知程度，结合数学期望公式（Exp(x) = mci×P + (1-mci)×L），可量化单笔交易的盈利概率与风险边界。在趋势跟踪策略中，概率论还可用于识别价格突破关键均线的有效性。

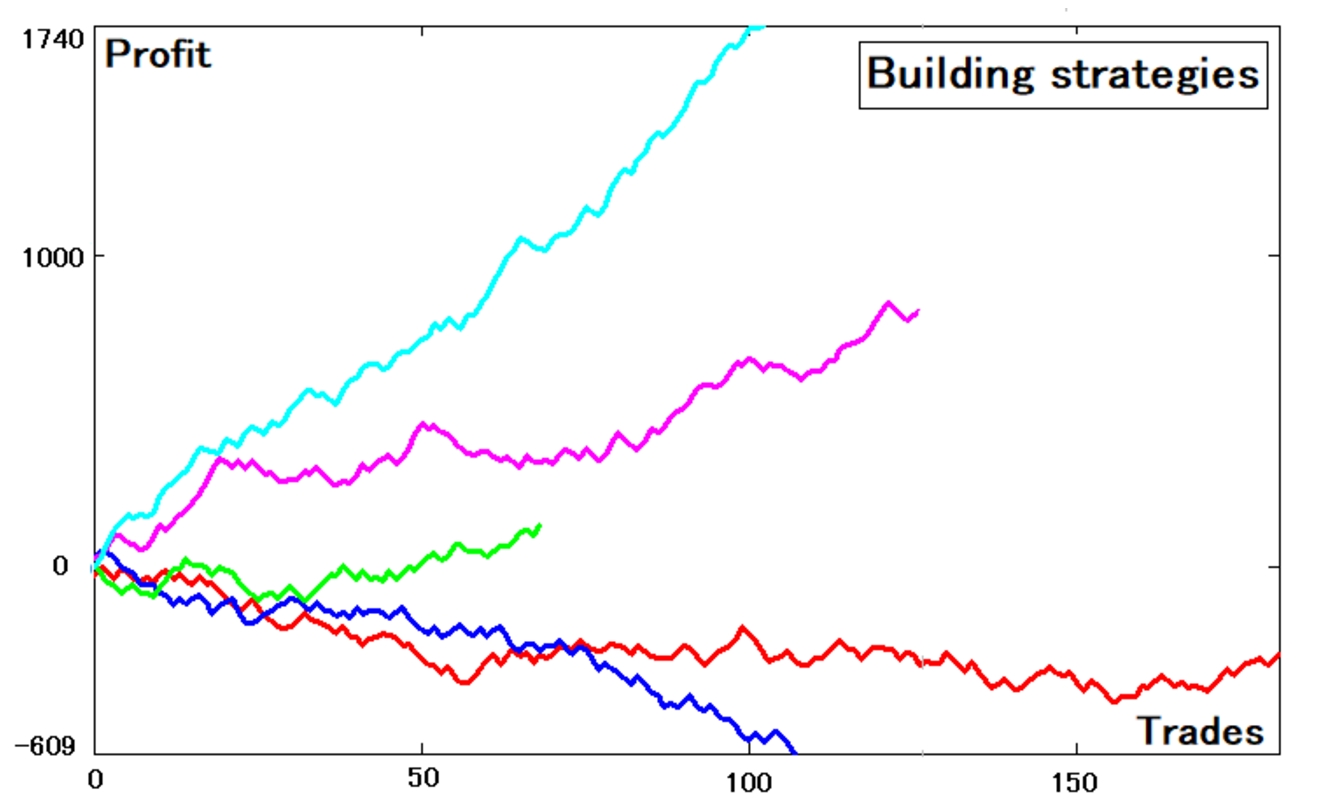
　　二、交易策略的简化与数学建模

　　1. 从多重状态到双重状态的转换

　　复杂交易系统常包含大量中间状态（如部分止盈、止损调整等）。通过引入等距止损级别与分形框架，可将策略简化为仅有“盈利”与“亏损”两种结果的二元模型。例如，设定固定止损/止盈点位后，每笔交易的最终结果仅取决于价格是否触及阈值，从而大幅降低状态空间复杂度。

　　2. 分形公式与概率模型的结合

　　基于简化后的二元状态，应用分形公式计算策略的极限时间与偏移量：

　　- 时间极限：(T(n) = \lim_{n \to \infty} \left[ (P_1 T_1 + (1-P_1)T_2) \cdot n \right] \)

　　- 价格偏移：( P(n) = \lim_{n \to \infty} \left[ (P_1 Pr - (1-P_1)Pr) \cdot n \right] \)

　　其中，( P1 )为盈利概率，( T_1/T_2 )为盈利/亏损的平均生存期，( Pr )为步长参数。

　　三、数学模型的系统化构建

　　1. 方程组推导与参数求解

　　通过联立方程消除冗余变量，最终得到仅含\( P_1 \)、\( T_1 \)、\( T_2 \)的方程组：

　　\[

　　\begin{cases}

　　A_1 n = A_2 m \\

　　B_1 n = B_2 m

　　\end{cases}

　　\]

　　结合边界穿越概率相等的约束条件（如\( P_U = P_D \)）及平均时间公式：

　　\[T_{U/D} = S_{U/D,u} \cdot T_1 + S_{U/D,d} \cdot T_2\]

　　可解得关键参数。

　　2. 蒙特卡洛模拟验证

　　通过随机生成交易序列并模拟执行，可验证模型的稳定性。例如，在期货15分钟周期策略中，模拟显示胜率可达65%，回撤控制在15%以内。

　　四、实际应用与优化方向

　　1. 策略优化案例

　　- 案例1：期货趋势跟踪

　　参数：MA5（快速）+ MA20（中期）+ MA60（长期），规则为“多头：MA5>MA20>MA60”，胜率65%。

　　- 案例2：多指标融合策略

　　组合EMA12、SMA26与MACD，年化收益率提升至22%，减少震荡市假信号。

　　2. 改进方向

　　- 动态参数调整：根据市场波动率（如ATR指标）自适应调整均线周期。

　　- 多维度融合：结合波动率曲面、订单流数据优化仓位管理。

　　- 系统架构优化：采用分布式微服务架构降低延迟，支持高频交易。

　　组合数学与概率论为交易系统提供了从策略设计到风险管理的完整分析框架。使用MetaTrader5安卓版，通过简化状态空间、构建数学模型并验证实际效果，交易者可显着提升策略的鲁棒性。